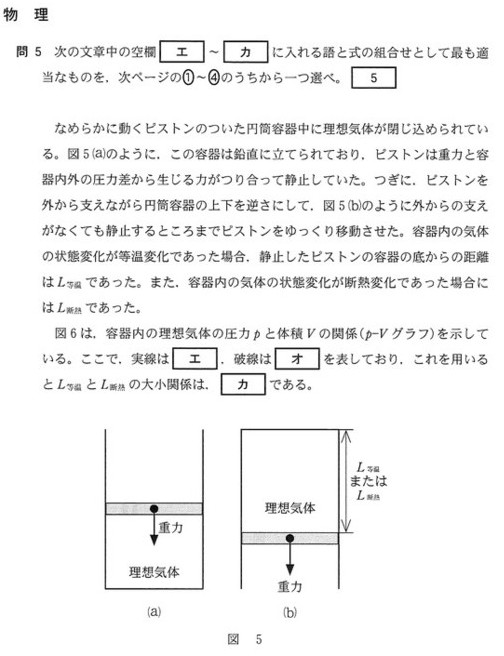
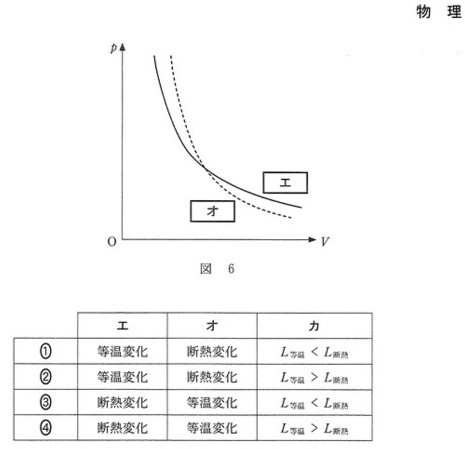

答えは、②です。
等温変化、断熱変化のP-Vグラフは頻出ですので、覚えておくと良いでしょう。
ーーー
それでは解答です。
(a)の状態から、(b)の状態になるには気体は膨張していますので、等温膨張と断熱膨張で考えます。
等温膨張は、ピストンの中の理想気体の温度\(T\)一定のまま体積\(V\)を膨張させる変化です。
この時、気体の状態方程式は温度\(T\)が一定ですから、\(PV=nRT=一定\)となり、P-Vグラフ上は体積\(V\)が大きくなった分圧力\(P\)が下がる反比例の双曲線になります。
等温膨張をする際は、外から熱を取り入れて、その分仕事つまり膨張することになり、温度変化がないので内部エネルギーの変化はありません。
次に断熱膨張ですが、断熱状態ですので外部から熱を取り込むことができません。
外から熱を取り込めませんので、膨張する分の仕事は気体の内部エネルギーを使うことになり、気体の温度が下がります(気体の内部エネルギーは温度に比例します)。
気体の状態方程式\(\displaystyle\frac{PV}{T}=nR=一定\)を考えますと、体積\(V\)が膨張し温度\(T\)が下がる分を相殺するほど圧力\(P\)が下がることになります。つまり、等温変化よりも、温度\(T\)が下がる分大きく圧力\(P\)を下げる必要があります。
よって、P-Vグラフ上で膨張つまり体積\(V\)が大きい領域で、断熱変化は等温変化よりも圧力\(P\)が下になるグラフとなります。
したがって、解答はエ:等温変化 オ:断熱変化 となり、解答は①②にしぼられます。
つぎに、(b)の状態ですが、重力と理想気体の圧力\(P\)がつりあっていますので、等温膨張、断熱膨張どちらの状態のときも、理想気体の圧力\(P\)は重力と同じということに成ります。
よって、体積\(V\)が膨張している領域で、同じ圧力\(P\)が同士を比較すれば良いわけです。
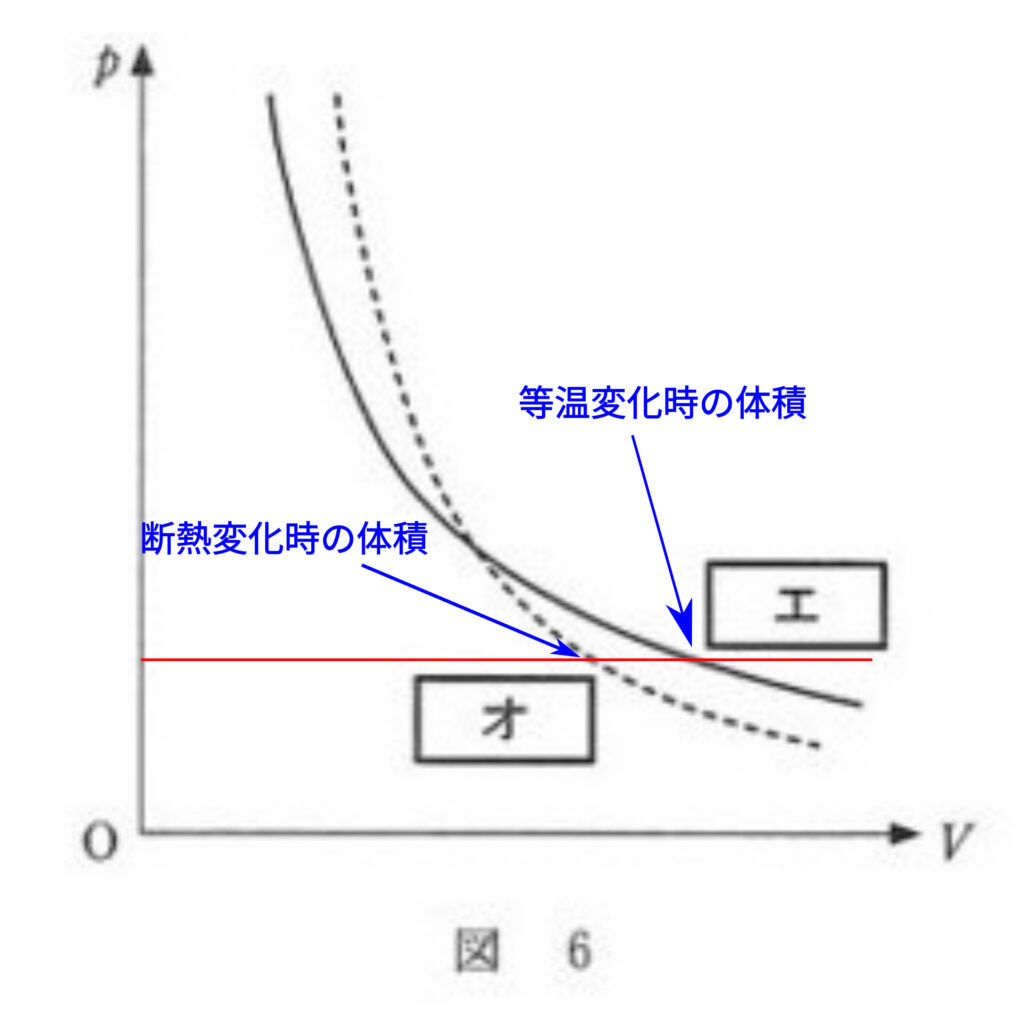
上図で、同じ圧力\(P\)が同士を比較すると、\(等温変化時の体積>断熱変化時の体積\) となっています。
ピストンの断面積は一定ですので、体積の大小はそのまま、容器の底からの距離\(L\)の大小の関係となりますので、\(L_{等温} > L_{断熱}\)となります。よって解答は②です。
他にも大学共通テストの解答の記事がありますので、よかったら見てくださいね。

初稿:2021-2-14
数式修正:2021-2-22




コメント