2021年　大学入学共通テスト　物理　第2問　問1〜3

答えは、6：③、　7：③、　8：0、　9：①　です。

この問題は、コンデンサの性質や、オームの法則、キルヒホッフの法則の知識が必要ですね。

オームの法則については、下記の動画がよく説明されていますので、よかったらご覧ください。２０分くらいですよ。

NHK高校講座　基礎物理

第32回第２編　さまざまな物理現象とエネルギー　電流の大きさを決めるもの　～電流・電圧・電気抵抗～

ーーー

それでは、解答です。

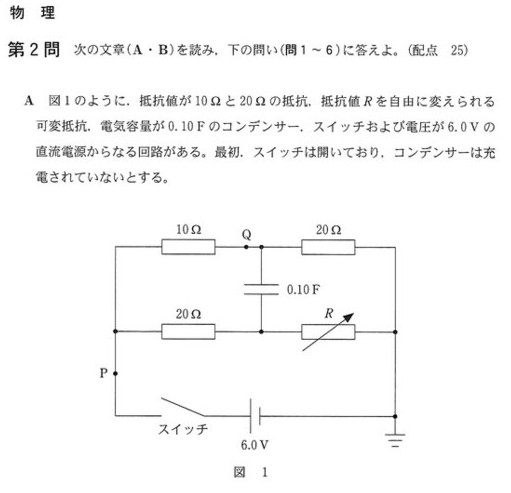
コンデンサに電荷が蓄えられてない状態で、スイッチを入れると、コンデンサーはできるだけの多くの電荷を蓄えようとします。

つまり大きな電流がコンデンサに流れ込むことに成ります。

コンデンサの両端の電圧が0の状態で電流が大きいということは、オームの法則\(V=RI\)よりコンデンサは見かけ上抵抗値が0とみなせますので、コンデンサの両端を短絡しても同じですね。

可変抵抗値\(R=10\)で、コンデンサの両端が短絡されているのと同じ回路は③ですので、6：③　となります。

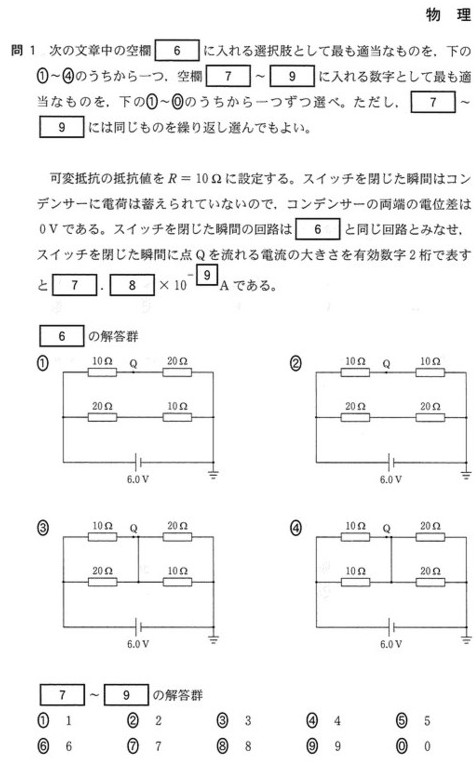
さて、次に点Qを流れる電流ですが、回路③で考えるとすぐ解けます。

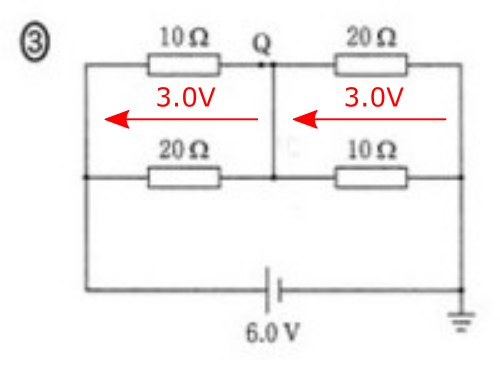
上図のように、\(10Ω\)と\(20Ω\)の抵抗が並列接続されているものが、２つ直列接続されていることになります。

よって、直列接続されている部分は同じ抵抗値（両方共\(10Ω\)と\(20Ω\)の抵抗が並列接続）ですから、電池の電圧が半分ずつ、つまり\(3V\)ずつかかります。

したがって、点Qを流れる電流値はオームの法則より\(I=\displaystyle\frac{V}{R}=\frac{3.0}{10}=0.30=3.0\times10^{-1}A\)となります。

よって、解答は　7：③、　8：0、　9：①　となります。

ーーー

答えは　10：④、　11：②、　12：④、　13：0、　14：①　です。

こちらも問1と同じ分野の知識が必要とされますね。

もしホイートストンブリッジ回路を高校でも習うのであれば、知っていると楽に解けますが知らなくてもこの問題は解けますのでご安心を。

ーーー

それでは解答です。

まず、問２です。

可変抵抗値\(R=10\)のままで、スイッチを入れたまま十分時間が経過してコンデンサに流れ込む電流が0になったのですから、オームの法則\(V=RI\)を考えるとコンデンサが無限に大きな抵抗値になったと同じと考えても同じです。

つまり、回路的にはコンデンサを外してしまっても同じですので、問1の①の回路と同じ回路を考えれば良いことに成ります。

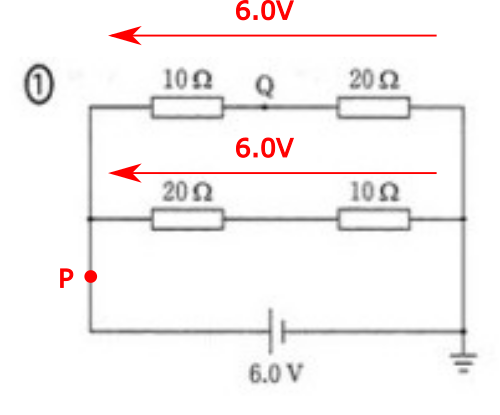
上図は問1の①の回路です。

こうなってしまえば、点Pを流れる電流を求めるのは簡単です。

各\(10Ω\)と\(20Ω\)の抵抗が直列接続になっている部分に、電池の電圧がそれぞれ\(6V\)ずつかかりますので、オームの法則より\(I=\displaystyle\frac{V}{R}=\frac{6.0}{10+20}=0.20A\)の電流が流れます。

点Pには、それぞれの各\(10Ω\)と\(20Ω\)の抵抗が直列接続になっている部分に流れる電流の合計、つまりこの場合は２倍ながれますので、\(0.20\times 2=0.40A\)となり、10：④　となります。

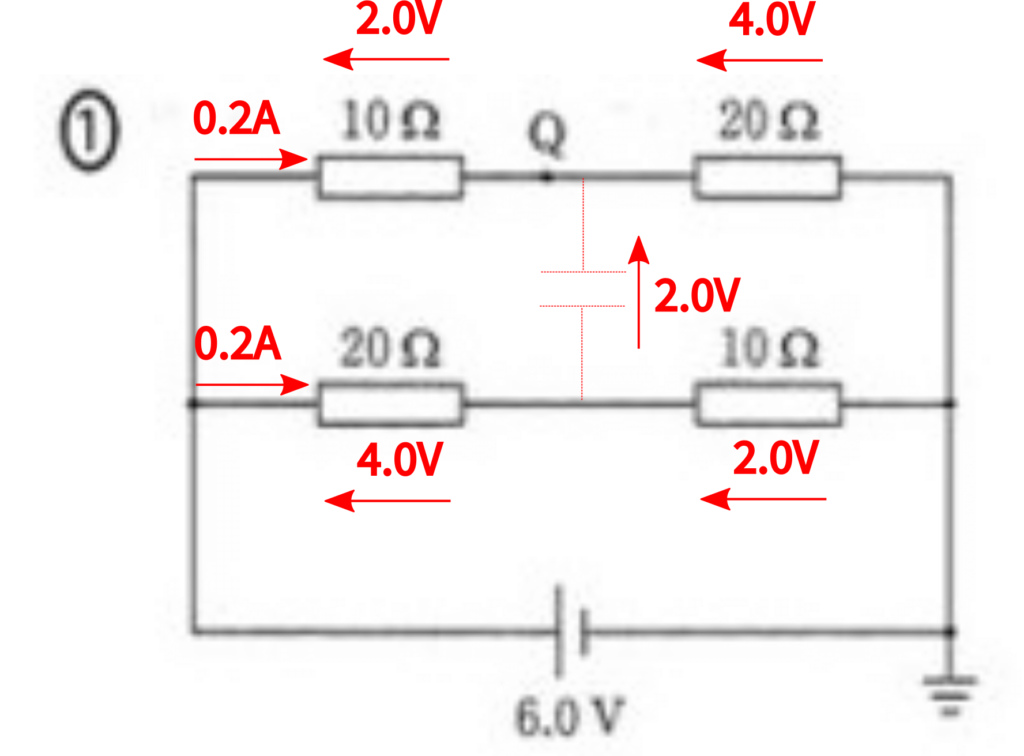
さて、求めた電流\(0.2A\)を用いてオームの法則で（分圧で求めてもいいです）それぞれの抵抗にかかる電圧を求めますと、上図のようにコンデンサにかかる電圧は\(2.0V\)となります。

従いまして、コンデンサの電気容量\(C=0.10F\)とコンデンサにかかる電圧\(V=2.0V\)から、コンデンサに蓄えられた電気量\(Q\)は、\(Q=CV=0.10\times2.0=0.20C\)となり、11：②　が正解です。

次は、問3です。

問1、問2と解いてきて、スイッチを入れた直後と十分時間が立った後でコンデンサにかかる電圧が変わってますね。

スイッチを入れた直後でも、十分時間が立った後でも、コンデンサの両端の電位が一緒になるようにすれば、コンデンサにかかる電圧は0となり、コンデンサに流れ込む電流もありませんから、コンデンサは無いも同然です。

そのような状態になるように可変抵抗\(R\)を調節してやる問題ですね。

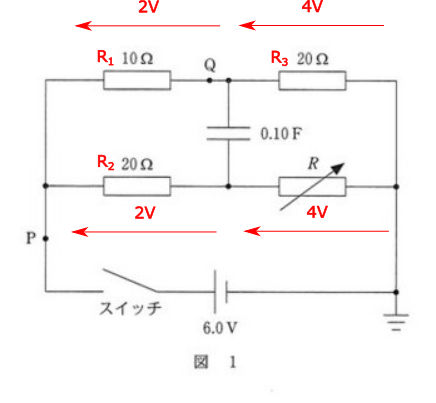
上図をみてください。

問２を解いて、スイッチを閉じて十分時間が立つと最終的に抵抗\(R_1\)には\(2V\)、抵抗\(R_3\)には\(4V\)がかかった状態になるのでした。

ここで抵抗\(R_2\)に\(2V\)、可変抵抗\(R\)に\(4V\)がかかっている状態になれば、コンデンサの両端の電位が一緒になりますから、コンデンサにかかる電圧は0です。

この状態にするには、可変抵抗\(R\)の値を、なれているならば\(R_2\)の２倍の抵抗値\(R=R_2\times2=40Ω\)とすれば良いことがわかります。

抵抗\(R_2\)に流れる電流\(I\)をオームの法則から\(I=\displaystyle\frac{V}{R_2}=\frac{2.0}{20}=0.1A\)と求めてから、この電流\(I=0.1A\)が可変抵抗\(R\)に流れて電圧が\(4V\)なのだから、可変抵抗値はオームの法則より\(R=\displaystyle\frac{V}{I}=\frac{4.0}{0.1}=40Ω\)と求めてもよいです。

さらにさらに、ホートストンブリッジ回路を習っているのであれば、コンデンサを検流計に見立てて、コンデンサに流れる電流が0になるように可変抵抗\(R\)を調節すると考えると、ホイートストンブリッジの平衡条件より、\(R=\displaystyle\frac{R_2R_3}{R_1}=\frac{20\times 20}{10}=\frac{400}{10}=40Ω\)と、一発で答えが導き出せます。

答えに合うように\(R=40=4.0\times10^1Ω\)とすると、答えは　12：④、　13：0、　14：①　です。

他にも大学共通テストの解答の記事がありますので、よかったら見てくださいね。