
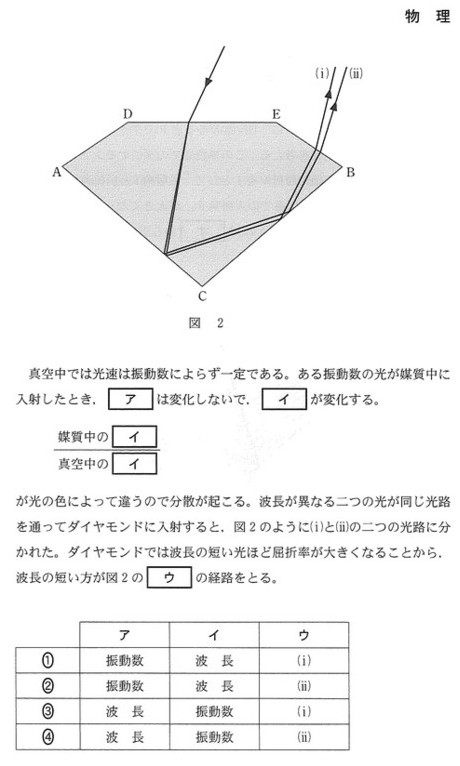

問1の答えは①となります。
この問題は文字通り、光の屈折率の知識が必要となります。
―――
それでは解答です。
光の性質として、真空中の光が媒質に入射した時、光の速度\(c\)が遅くなります。
そして、これは高校の勉強の範囲から外れてしまうと思うのですが、光の粒子である光子の持つエネルギーは光の振動数\(ν\)(ギリシャ文字でニューとよみます)に比例します(光電効果は高校で習うのかな?)。
媒質に入射する前後でエネルギーは保存されますので、入射前後で光の振動数\(ν\)は変化しません。
速度\(c\)、振動数\(ν\)(ギリシャ文字でニューとよみます)、波長\(λ\)の関係は\(c=νλ\)ですから、真空から媒質に入射した際、光の速度が遅くなるのは、波長が短くなるからということになります(振動数は変化しないので)。
これで選択肢は、①②に絞られます。
まあ、光の振動数は異なる媒質に入射しても変わらないと光の性質として覚えておくしかないですかね、今のうちは。
さて、屈折率の大小で光はどのように進むのでしょうか?
図に屈折率の大小で光がどのように進むかを示してみました。
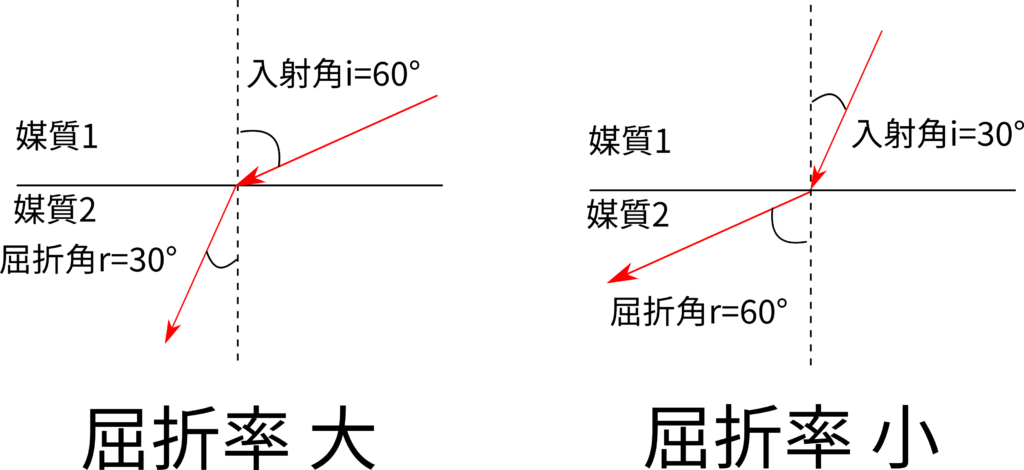
屈折率は、入射角\(i\)と屈折角\(r\)から、\(\displaystyle\frac{\sin i}{\sin r}\tag{1}\)であらわされるのでしたね。
それでは、図の屈折率を計算してみましょう。
簡単のために、角度は\(60^\circ\)と\(30^\circ\)にしましたので、\(\sin 60^\circ=\displaystyle\frac{\sqrt{3}}{2}\)、\(\sin 30^\circ=\displaystyle\frac{1}{2}\)ですから、
上図左側の屈折率は\(\displaystyle\frac{\sin 60^\circ}{\sin 30^\circ}=\displaystyle\frac{\displaystyle\frac{\sqrt{3}}{2}}{\displaystyle\frac{1}{2}}=\sqrt{3}\)、右側の屈折率は\(\displaystyle\frac{\sin 30^\circ}{\sin 60^\circ}=\displaystyle\frac{\displaystyle\frac{1}{2}}{\displaystyle\frac{\sqrt{3}}{2}}=\displaystyle\frac{1}{\sqrt{3}}\)となり、
左側が屈折率 大、右側が屈折率 小ということになります。
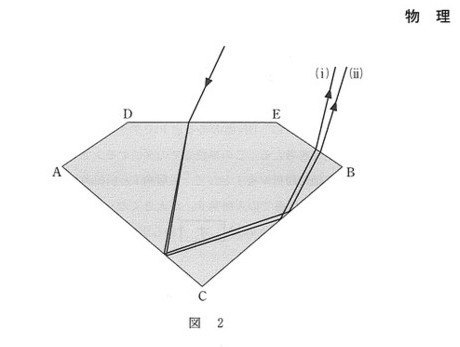
よって、ダイヤモンドに入射したときに、屈折角がより小さい方が屈折率が大きいことになりますので、経路iが屈折率が大きいということになり、問1の答えは①となります。
―――
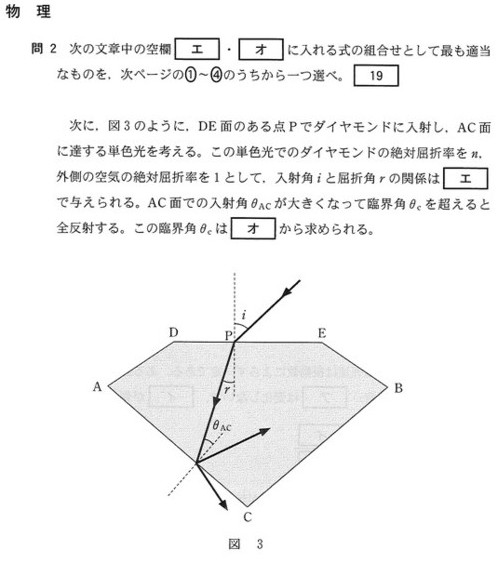

問2の答えは②となります。
この問題は絶対屈折率と全反射およびその臨界角の知識が必要となります。
でも、そんなに難しいことはありませんよ。
ちなみに問1の屈折率は相対屈折率といいますが、入射する側の媒質を真空として、入射される側の媒質aとして屈折率を表したものを媒質aの絶対屈折率といってますよ。
真空を基準に表しておく感じですね。
―――
それでは解答です。
媒質の絶対屈折率と、入射角、屈折角には次の関係があります。これは覚えちゃった方が速いし間違えにくいので暗記しちゃいましょう。
絶対屈折率\(n_1\)の媒質1から入射角\(i\)で絶対屈折率\(n_2\)の媒質2へ入射し、屈折角\(r\)のとき、\(n_1\sin i=n_2\sin r\tag{2}\)の関係があります。
記号・数字の入れ替えもなく、順番的に覚えやすいですよね。
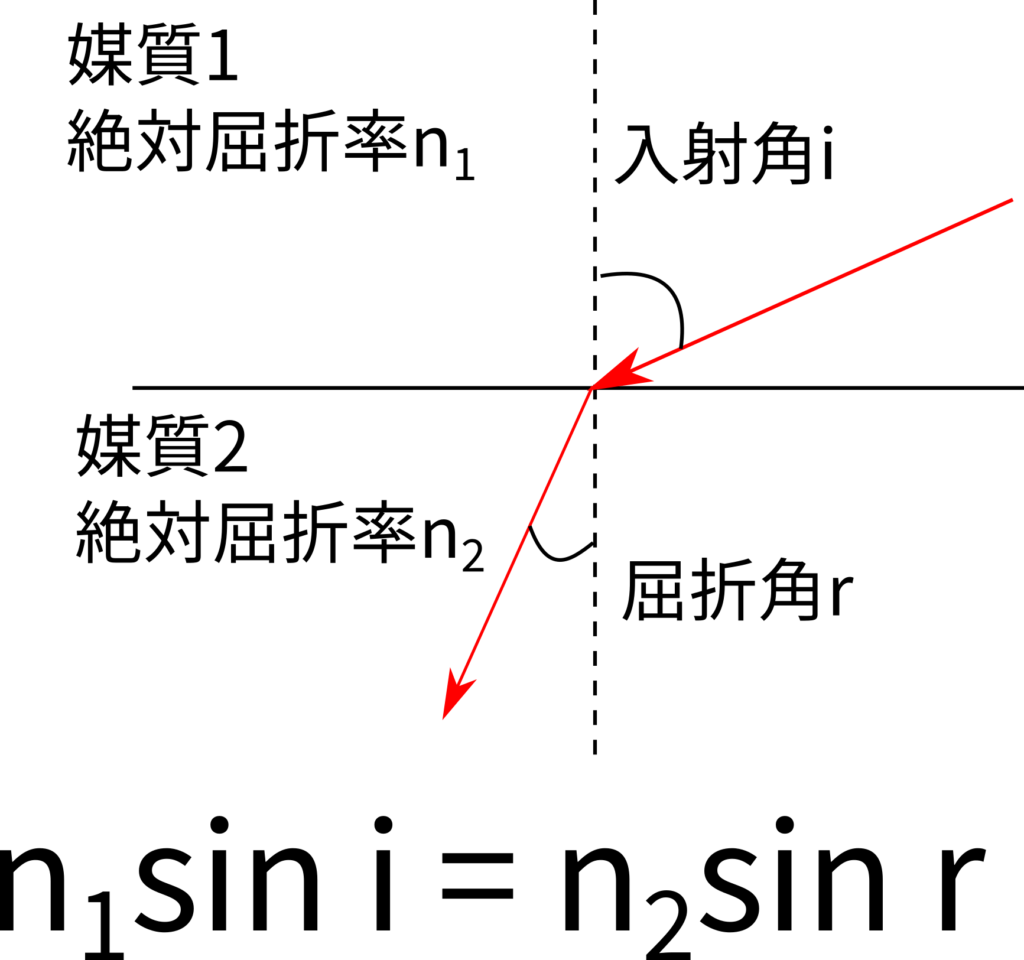
ちなみに問1でやった相対屈折率との関係は、相対屈折率を\(n_{12}\)とすると、\(n_{12}=\displaystyle\frac{\sin i}{\sin r}=\frac{n_2}{n_1}\)となりますが、これは暗記しなくても式(1)(2)から導出できますよ。
さて、ダイヤモンドの絶対屈折率\(n\)、空気の絶対屈折率を1として、空気からダイヤモンドに入射するときの関係は式(2)に、\(n_1=1\)、\(n_2=n\)を代入してやれば入射角\(i\)と屈折角\(r\)の関係は\(\sin i=n\sin r\)となり、答えは①②に絞られます。
つぎに、臨界角ですが次の図をみてください。
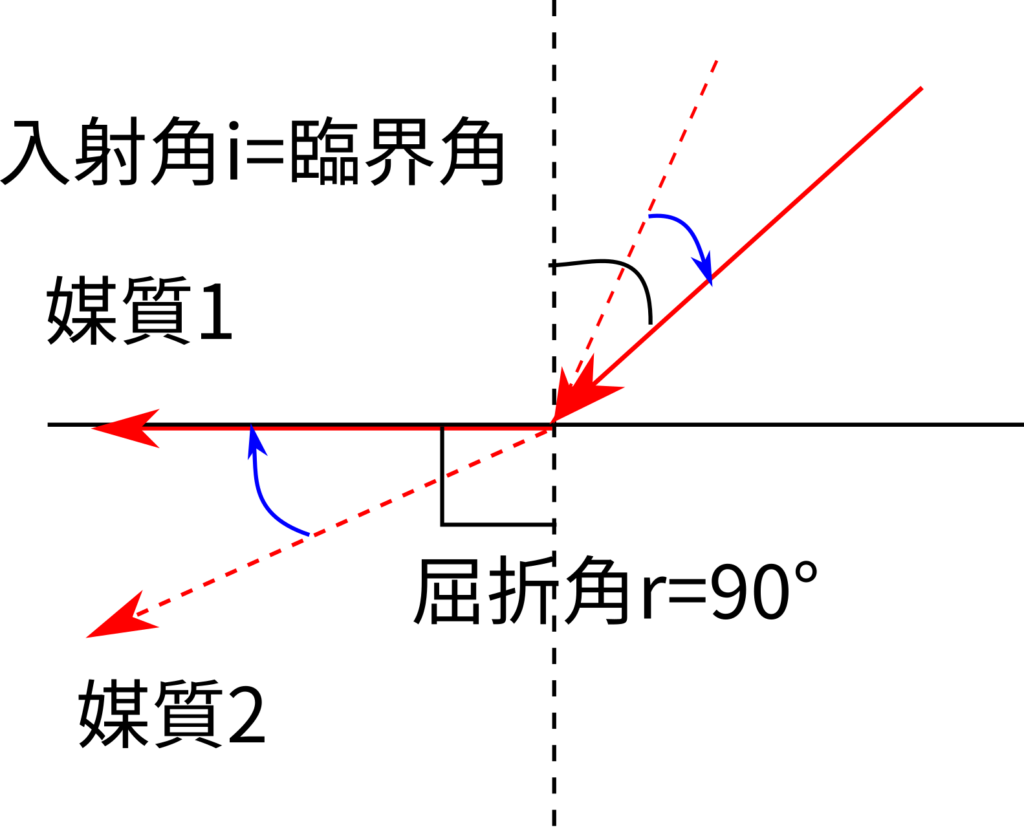
入射角をどんどん大きくしていくと、屈折角もどんどん大きくなっていきます。
やがて屈折角が\(90^\circ\)になると媒質2に光が入射しないことになります。
このときの入射角を臨界角といいます。
以上のことをふまえて、\(AC\)面を考えて
媒質1:ダイヤモンド 絶対屈折率\(n\)、入射角\(θ_C\)、
媒質2:空気 絶対屈折率1、屈折角\(90^\circ\)
を式(2)に代入しますと、\(n\sin θ_C=\sin 90^\circ=1\)ですから、\(\sin θ_C=\displaystyle\frac{1}{n}\)となり問2の答えは②となります。
式(2)なかなか便利ですね。
―――
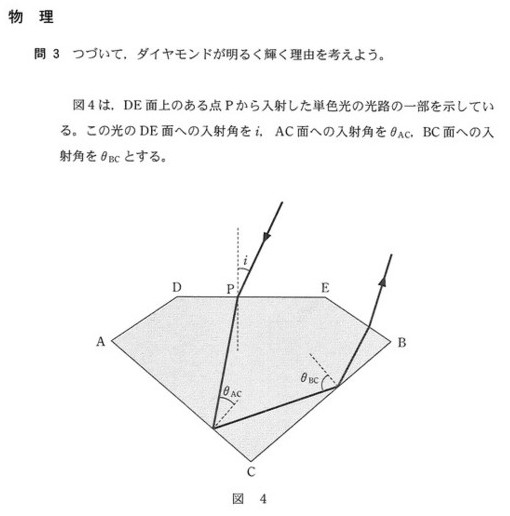

問3の答えは 20:④、 21:①となります。
この問題は、結構問題文にヒントがアリアリですので、よく問題文を読むことが肝要ですね。
ま、それはどんな問題を解くことにも言えますかねw
後は慌てずグラフを読むことですよ。
―――
それでは解答です。
まずは20の解答です。
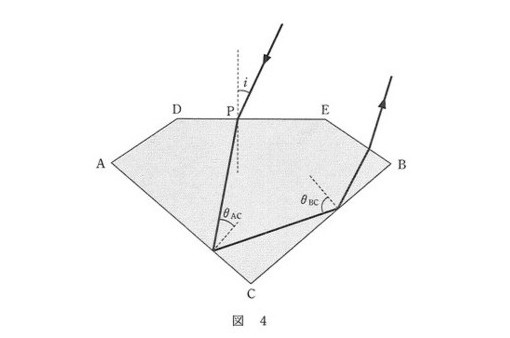
問2で解説したように、入射角をどんどん大きくしていって、屈折角が\(90^\circ\)になったときの入射角が臨界角です。
そしてそして、問2の問題に「\(AC\)面での入射角\(θ_{AC}\)が大きくなって臨界角\(θ_C\)を超えると全反射する」とあります。
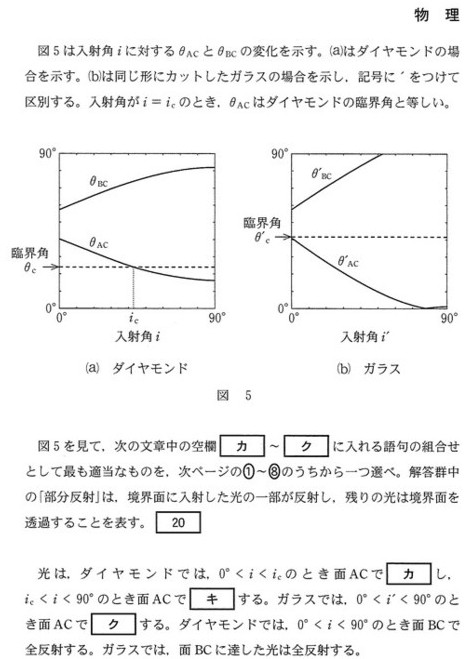
はい、ここで図5の(a)ダイヤモンド の\(θ_{AC}\)のグラフに注目です。
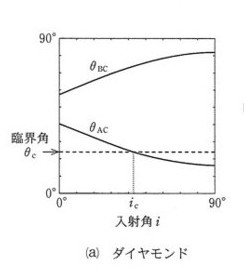
\(θ_{AC}\)がどんどん大きくなるのは、入射角\(i\)を小さくする方向ですね。
つまり、\(i\)が大きい\(i_C <i<90^\circ\)の範囲のときは、\(θ_{AC}\)が小さいので、部分反射するわけですよ。
そして、\(i\)をどんどん小さくしていって\(i=i_C\)のとき\(θ_{AC}=θ_C\)となり、臨界角になるわけです。もちろん屈折角が\(90^\circ\)です。
それから、さらに\(i\)をどんどん小さくしていって\(θ_ {AC}\)は臨界角を越えてますから、全反射するわけです。
ということで、カ:全反射、キ:部分反射 ということになりますから、選択肢は③④にしぼられます。
つぎに図5の(b)ガラス の\(θ’_{AC}\)のグラフに注目です。
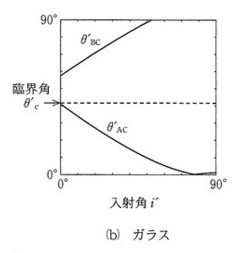
\(θ’_{AC}\)は、全範囲にわたって臨界角\(θ’_C\)より小さいです。
つまり、\(i\)の全範囲\(0^\circ <i'<90^\circ\)で部分反射することになります。
よって、20:④ ということになります。
はい、最後は21の解答ですが、ここまで解答してきた人には、サービス問題ですよ。
問2の最後のところで\(AC\)面を考えて
媒質1:ダイヤモンド 絶対屈折率\(n\)、入射角\(θ_C\)、
媒質2:空気 絶対屈折率1、屈折角\(90^\circ\)
として、\(\sin θ_C=\displaystyle\frac{1}{n}\)という関係を導きましたね。
屈折率が大きいほど、臨界角が小さいという関係がわかります。
従いまして、ダイヤモンドはガラスより屈折率が「大きい」ため臨界角が小さい、ということがわかりますよね。
答えが書いてありましたね。
ということで、選択肢は①②にしぼられます。
それから、入射角の広い範囲で二度「全反射」し、観察者のいる情報に進む光が多い、となりますよね。
20で、ダイヤモンドは面\(BC\)で全範囲\(0^\circ <i<90^\circ\)で全反射してますから、面\(AC\)で全反射すれば「二度」になりますよね。
どうやっても二度、部分反射できませんね。
ということで、21:①が解答となります。サービスですねー、ありがたや。
他にも大学共通テストの解答の記事がありますので、よかったら見てくださいね。

初稿:2021-2-24




コメント