
答えは、② です。
この問題は、ファラデーの電磁誘導の法則とレンツの法則を理解している必要があります。
「1つの回路に生じる誘導起電力の大きさはその回路を貫く磁束の変化の割合に比例し(ファラデーの電磁誘導の法則)、その時生じる誘導電流は磁束の変化を妨げる方向に流れる(レンツの法則)」と言うやつですね。
この導体棒が移動する問題(コの字の針金上を移動するものが多いですが)は、頻出問題ですので、慣れておくことをおすすめします。
ーーー
それでは解答です。
まずは、誘導電流の方向です。
2本の金属レールと導体棒a、bで構成される1つの回路を考えます。
回路を鉛直上向きの一様な磁束が、磁束密度\(B\)で貫いています。
導体棒aが右側に動くことによって、この回路を貫く鉛直上向きの磁束が増える変化をすることになります。
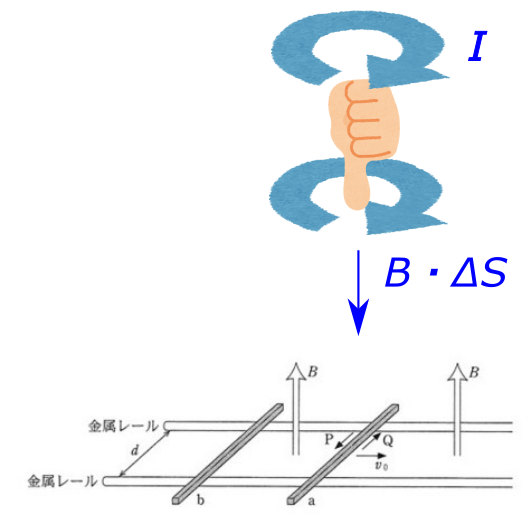
ということは、レンツの法則により誘導電流は、上向きに増える磁束を妨げる向きに生じるわけです。右ねじの法則で!!
上図を見てください。
上向きに増える磁束を妨げる向き、つまり下向きの磁束を増やしてなんとか上向きの磁束が増えるのを妨げるために、右ねじの法則で誘導電流が生じるのです。
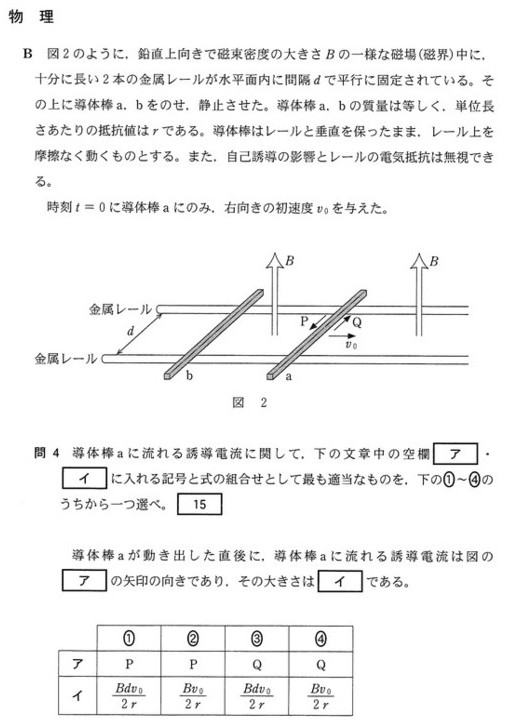
よって、誘導電流はPの方向に流れます。よって ア:P となり、選択肢は①②にしぼられます。
次に誘導電流の大きさを求めるために、誘導起電力(電圧)を求めることとします。
ファラデーの電磁誘導の法則によって、誘導起電力\(V\)は、\(Δt\)秒間に変化する磁束を\(ΔΦ\)とすると\(V=\displaystyle-\frac{ΔΦ}{Δt}\)と表されるのでしたね。マイナスは磁束の変化を妨げる向きに生じるという意味です。方向はもう解っているので、誘導起電力の大きさだけ知りたいので以下はマイナスを省略しますよ。
さて、磁束の変化分\(ΔΦ\)は、磁束密度\(B\)を用いて表現すると\(ΔΦ=B\cdotΔS\)となりますので、誘導起電力は\(V=\displaystyle\frac{ΔΦ}{Δt}=B\cdot\frac{ΔS}{Δt}\)となります。\(ΔS\)は導体棒aが右側に動くことによって増加する回路が囲む面積です。
ここで、\(\displaystyle\frac{ΔS}{Δt}\)の部分は、\(Δt\)秒間に変化する面積\(ΔS\)ということですので、金属レール間の距離\(d\)と導体棒aの速度\(v_0\)を使って\(\displaystyle\frac{ΔS}{Δt}=dv_0\)となりますね?(速度は単位時間あたりに進む距離ということを考えるとわかりますよね)。
よって、誘導起電力の大きさは、\(V=\displaystyle\frac{ΔΦ}{Δt}=B\cdot\frac{ΔS}{Δt}=Bdv_0\)となります。
さて、後は回路の抵抗がわかれば誘導電流がわかりますよ、オームの法則で。
金属レールの抵抗値は問題より0、導体棒a,bは単位長さあたりの抵抗値が\(r\)ですから、導体棒a,bの長さがそれぞれ\(d\)であることを考慮すると、回路の抵抗\(R\)は\(R=2dr\)です。
よって、誘導電流\(I\)の大きさはオームの法則より、\(I=\displaystyle\frac{V}{R}=\frac{Bdv_0}{2dr}=\frac{Bv_0}{2r}\)となります。
したがって、答えは② です。
妨げる向き、重要ですので\(V=\displaystyle-\frac{ΔΦ}{Δt}\)のマイナス記号の意味を忘れないでくださいね。
なぜ、妨げる向きなのかというと、どうも自然は変化を嫌う性質があるようですよ。慣性の法則も変化を嫌うようですしね。
ーーー
答えは、問5:③、 問6:③ です。
これらの問題を解くには電磁力(ローレンツ力)や等加速度直線運動の知識が必要となります。
白くま父さんはフレミングの左手の法則があまり好きではないので、ほとんど右ねじの法則で考えます。
その方が物理的イメージが浮かぶからですね。
ーーー
それは、解答です。
まず、問5です。
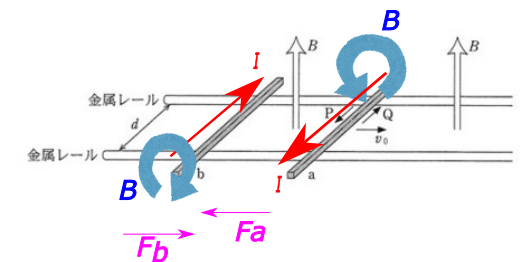
問4でPの向きに誘導電流が流れることがわかりましたので、導体棒a、bには上図のように誘導電流が流れ、導体棒a、bの周りには右ねじの法則にしたがって、磁界が生じます。
その結果、導体棒a、bの周りに生じた磁界によって、回路の外側の磁界は強められ密度が高くなり、回路の内側の磁界は弱められ密度が低くなります。
この磁界の密度の高低を解消しようと、密度の高い方から低い方へ導体棒a、bを動かす方向へ電磁力が働きます。
つまり、回路の内側の向きに働きます。図の\(F_a\)、\(F_b\)がそれです。力の向きは反対なので選択肢は③④に絞られますが、力の源になっている誘導電流は同じ大きさなので、力の大きさは同じになりますから、答えは問5:③です。
次に問6です。
すでに初速\(v_0\)で右向きに移動している導体棒aは、問5で解ったように左向きの電磁力\(F_a\)を受け、減速していきます。
また、導体棒bは右向きの電磁力\(F_b\)を受け、初速0から加速していきます。もちろん、右向きに移動するわけです。
ということで、導体棒bの速度が−になっている、つまり左向きになっている①②は選択肢から外れ、正解は③④にしぼられます。
さて、これらの加減速がいつまで続くかと言うと、導体棒a、bの速度が同じになるまでです。
導体棒a、bの速度が同じになると、回路の面積の変化は無くなりますので、誘導電流は発生しなくなり、電磁力\(F_a\)、\(F_b\)も無くなります。
最終的に導体棒a、bは等速直線運動をするようになるわけです。やっぱり、自然は変化を嫌うんですよ。
それでは、導体棒a、bの最終的な速度\(v\)を求めてみましょう。
電磁力\(F_a\)、\(F_b\)による加減速度を\(a\)とします。
導体棒aの最終的な速度\(v\)は、最終的な時間を\(t\)とすると、\(v=v_0-at\)と表されます(減速されているので、加速度は−です)。
導体棒bの最終的な速度\(v\)は、\(v=at\)と表されます(初速は0から加速します)。
はい、もう答えはでますね。2式から、\(at\)を消してやると、\(v=v_0-v\)なので、\(v=\displaystyle\frac{v_0}{2}\)となり、問6の答えは③です。
この問題は面白い問題ですね。導体棒aを初速\(v_0\)で動かすと、自然は変化を嫌って、変化を抑えるべく誘導電流を発生させ、導体棒aを減速、導体棒bを加速させ、最終的に面積の変化がない状態(安定状態)になろうとするんです。本当に自然はおもしろいですね。
他にも大学共通テストの解答の記事がありますので、よかったら見てくださいね。

初稿:2021-2-23




コメント