
答えは以下となります。
\(\displaystyle\frac{ア}{イ}=\frac{4}{5}\)
ウエ : 12
オカ : 12
キク : 25
この問題は、三角関数、余弦定理の知識が必要となります。
ーーー
それでは解答です。
まずは、\(\sin A\)を求めます。
問題に、\(\cos A= \displaystyle\frac{3}{5} \)がありますので、コレを使います。
解き方はぱっと浮かぶのは2つですね。
まず1つ目、このコサインをみたらパッとこの直角三角形が浮かぶくらいになっておくと良いでしょう。大学入試以外の試験でもよく出ますからね。
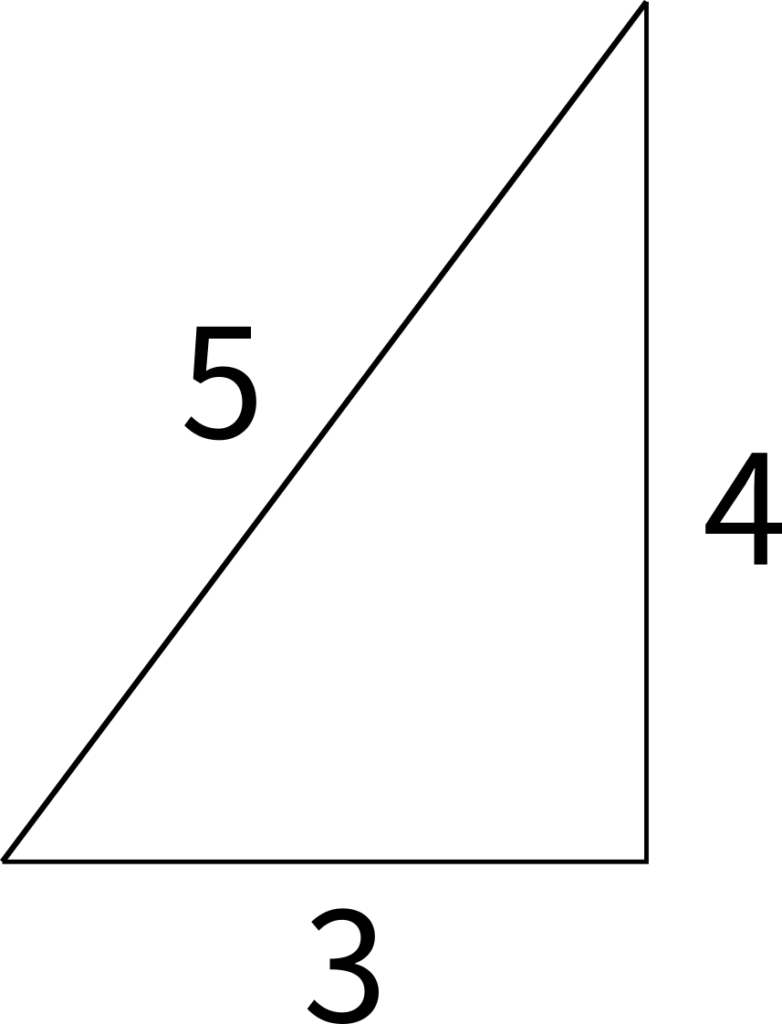
\(\cos A= \displaystyle\frac{3}{5} \)を満たしてますよね。もうすぐに、\(\sin A=\displaystyle\frac{4}{5}\)と解っちゃいます。
2つ目の解き方としては、\(\sin^2A + \cos^2A=1\)を使います。これをつかって、\(\sin A=\pm\sqrt{1-\cos^2A}\)と解いてやればいいです。
いずれでも、良いですが直角三角形を思い浮かべるほうが、白くま父さん好きですね。
ということで、\(\displaystyle\frac{ア}{イ}=\frac{4}{5}\)です。
つぎは、\(\triangle ABC\)の面積です。まず、分かっている寸法を入れておきますね。
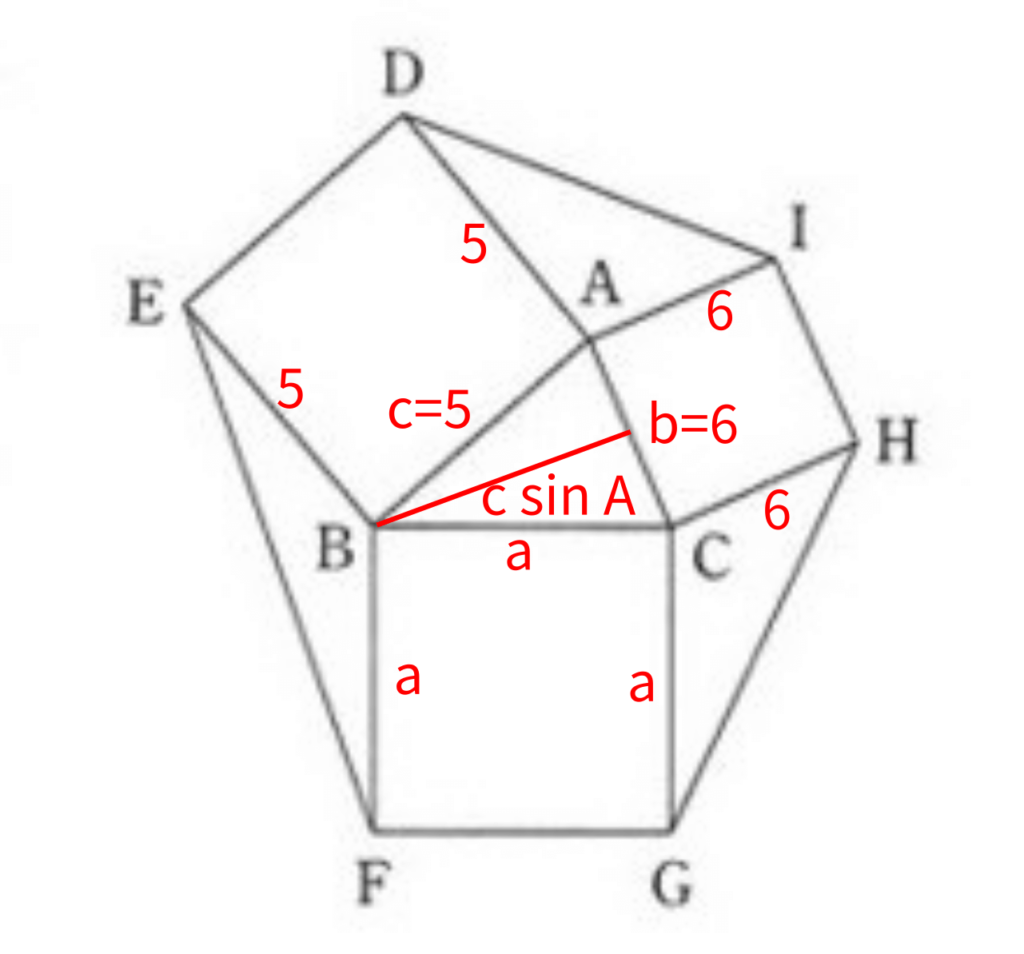
三角形の面積は、底辺x高さ÷2で求められるのは、学年が進んでも変わりません。
底辺は\(b\)、高さを\(c\sin A\)としてやれば、\(\triangle ABC=\displaystyle\frac{1}{2}bc\sin A=\frac{1}{2}\cdot6\cdot5\cdot\frac{4}{5}=12\) となります。
よって、ウエ : 12 です。
つぎは、、\(\triangle AID\)の面積です。\(\angle DAI\)が分かれば求められますね。
正方形ADEB、CHIAにより、\(\angle DAI=-\angle A\)ということになりますから、\(\triangle AID=\displaystyle\frac{1}{2}bc\sin -A=\displaystyle\frac{1}{2}bc\sin A=12\) となり、\(\triangle ABC\)と同じ面積になります。よって、オカ : 12 です。
さらにさらに同じ理由により\(\triangle BEF\)、\(\triangle CGH\)も同じ面積になります。
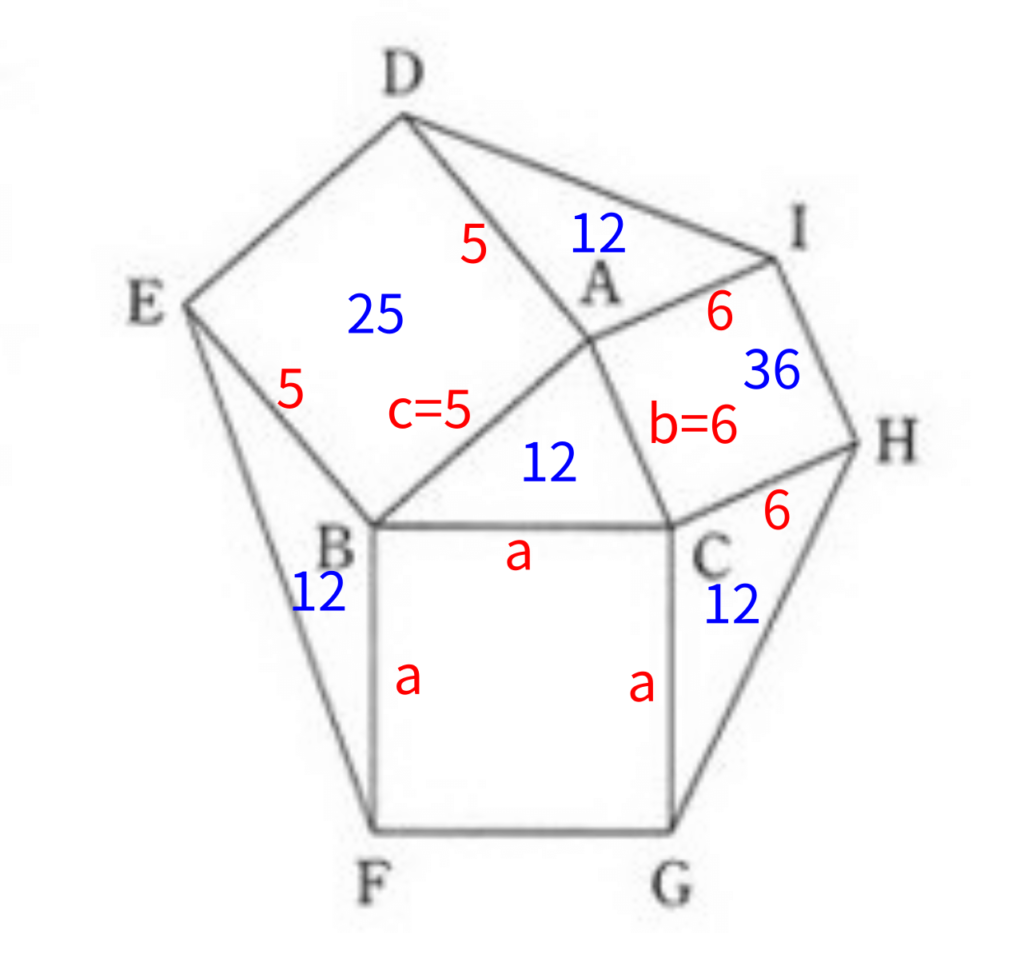
さて、最後に正方形BFGCの面積ですが、\(a\)が分かれば求まります。
これも2つの方法があります。
まず1つ目、\(\triangle ABC\)の面積が12と求まっていて、\(b=6\)で、高さが\(c\cdot\sin A=4\)ということですから、例のこの三角形の関係で、
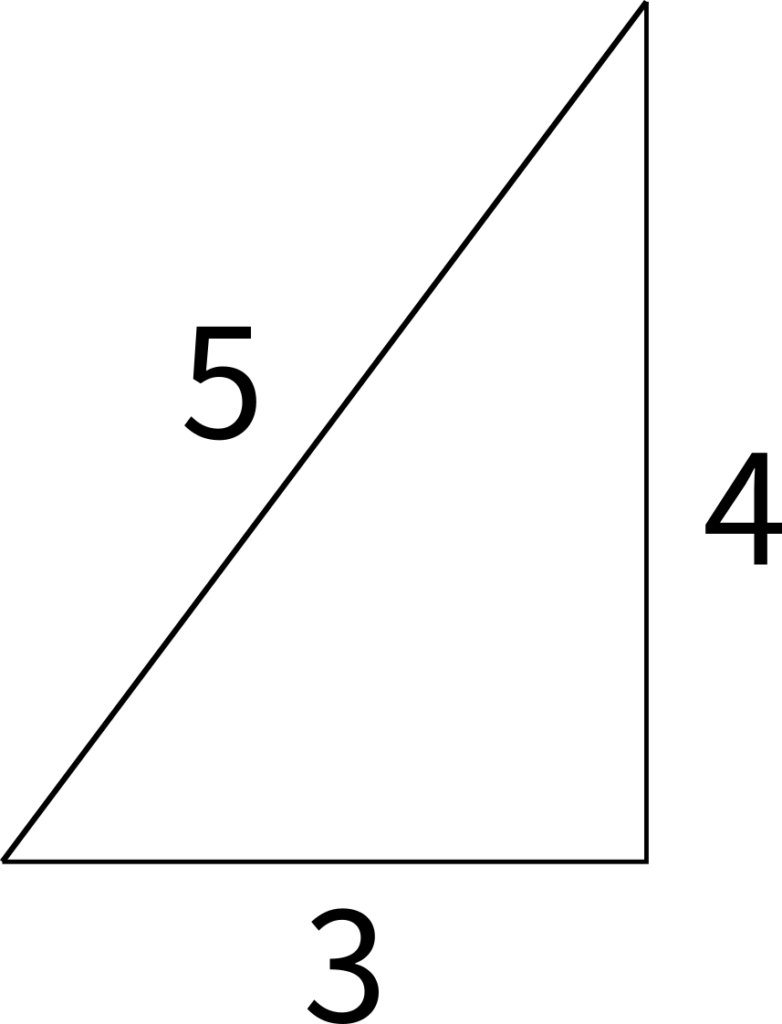
この三角形が2つくっついた形に\(\triangle ABC\)がなっていることに気づきます。つまり\(c=a=5\)の二等辺三角形です。
2つ目は、余弦定理をつかいます。\(a^2=b^2+c^2-2bc\cos A=36+25-2\cdot 5\cdot6\displaystyle\frac{3}{5}=25\)となります。
いずれの方法でも正方形BFGCの面積は、\(a^2=25\)と求めることが出来ます。
よって、キク : 25 です。
ーーー
答えは以下となります。
(2)ケ : ②、 コ : 0、 サ : ①
(3)シ : ③
この問題は余弦定理の知識が必要です。
ーーー
それでは解答です。
まずは(2)ですね。
\(S_1=a^2\)、\(S_2=b^2\)、\(S_3=c^2\)ですよね。
ここで余弦定理を使うと、\(a^2=b^2+c^2-2bc\cos A\)から、\(S_1-S_2-S_3=-2bc\cos A\)となりますね。
あとは答えが出てますよ。
- \(0^\circ<A<90^\circ\)のとき、\(\cos A\) は正、よって、\(S_1-S_2-S_3=-2bc\cos A\)は負となります。したがって解答は ケ : ②
- \(A=90^\circ\)のとき、\(\cos A=0\)、よって、\(S_1-S_2-S_3=-2bc\cos A\=0)。したがって解答は コ : 0
- \(90^\circ<A<180^\circ\)のとき、\(\cos A\) は負、よって、\(S_1-S_2-S_3=-2bc\cos A\)は正となります。したがって解答は サ : ①
以上で(2)は解答終了です。
つぎの(3)ですが、これは(1)でこの図の三角形はすべて同じ面積なのは解ってますので、答えは③となります。よって、(3)シ : ③ です。
ーーー
答えは、①となります。
この問題も、余弦定理と三角関数の知識を必要とするのですが、(1)〜(3)まででヒントが出てますので、問題ないと思います。
ーーー
それでは解答です。
六角形の各部の面積は、すでに\(b\)、\(c\)、\(\sin A\)、\(\cos A\)であらわされています。すなわち
- 4つの三角形の面積は、(1)の解答からそれぞれ\(\displaystyle\frac{1}{2}bc\sin A\)なので、合計は\(2bc\sin A\)です。
- 正方形CHIA、ADEBの面積はそれぞれ、\(b^2\)、\(c^2\)です。
- 正方形BFGCの面積は余弦定理により、\(a^2=b^2+c^2-2bc\cos A\)です。
あとは、これを全部足し合わせれば良いのです。つまり
\begin{eqnarray} & & b^2 + c^2 – 2bc\cos A + b^2 + c^2 + 2bc\sin A \\ &=& 2\{b^2 + c^2 +bc(\sin A – \cos A) \} \end{eqnarray}
です。よって、①が解答となります。
ーーー
答えは以下となります。
(5)セ : ②、 ソ : ②、 タ : 0、 チ : ③
(6)ツ : 0、 テ : ③
この問題は、正弦定理、三角形の内接円の知識を必要としますよ。
ーーー
それでは解答です。
まずは(5)です。
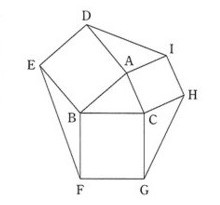
正方形ADEB、CHIAのため\(0^\circ<A<90^\circ\)のとき、\(90^\circ<\angle DAI<180^\circ\)です。
よって、\(ID>BC\)となり、セ : ②です。
さて、\(ID>BC\)なら、外接円の半径は \(\triangle AID > \triangle ABC\) になるに決まってますが、まあここは正弦定理をつかってちゃんとやってみましょう。
正弦定理は三角形の外接円の半径を\(R\)とした場合、\(\displaystyle\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R\)と表されます。\(2R\)までちゃんと覚えてますか?
さて、\(ID>BC\)なら、\(\displaystyle\frac{ID}{\sin A}>\frac{BC}{\sin A}\)ですから、外接円の半径は \(\triangle AID > \triangle ABC\)がいえますね。よかったよかった。ということで、ソ : ②です。
さて、このまま、外接円の半径のもっとも小さい三角形を場合分けで求めましょう。もちろん、正弦定理を思い浮かべながらですよ。
- \(0^\circ<A<B<C<90^\circ\)の時は、\(\triangle ABC\)が全部の辺が周りの三角形より小さくなるので、最も外接円の半径が小さくなります。よって、タ : 0。
- \(0^\circ<A<B<90^\circ<C\)の時は、\(GH\)が一番小さくなりますので、\(\triangle CGH\)が最も外接円の半径が小さくなります。よって、チ : ③。
つぎに(6)です。
三角形の内接円の半径\(r\)は、三角形の面積を\(S\)とすると、\(S=\displaystyle\frac{r}{2}\cdot (a+b+c)\)と表されます。
\(r\)について変形しますと、\(r=\displaystyle\frac{2S}{a+b+c}\)となります。
ここで、三角形の面積はすべて同じでしたから、3辺の合計が一番小さい三角形が、内接円の半径が一番大きいことになります。
ということは、場合分けも(5)タ・チと同じなので答えも(5)タ・チとおなじとなります。
よって、ツ : 0、 テ : ③ですね。
他にも大学共通テストの解答の記事がありますので、よかったら見てくださいね。

初稿 : 2021-3-26




コメント