
答えは、以下になります。
(1) \((アx+イ)(x-ウ)\) : \((2x+5)(x-2)\)
(2) \(\displaystyle\frac{-エ\pm\sqrt{オカ}}{キ}\) : \(\displaystyle\frac{-5\pm\sqrt{65}}{4}\)
\(\displaystyle\frac{ク+\sqrt{ケコ}}{サ}\) : \(\displaystyle\frac{5+\sqrt{65}}{2}\)
シ : 6
ーーー
それでは解答です。
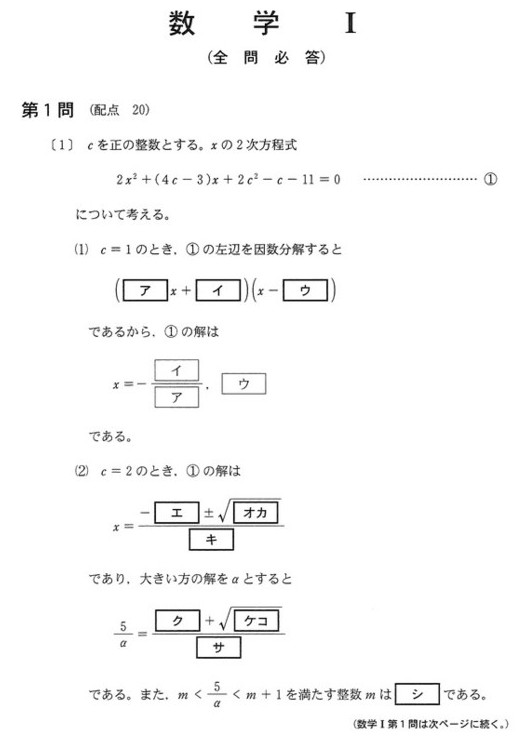
(1)\(c=1\)のとき、①の左辺は因数分解すると、以下となります。
\begin{eqnarray} & & 2x^2+(4\cdot1-3)x+2\cdot1^2-1-11 \\ &=& 2x^2+x-10 \\ &=& (2x+5)(x-2) \end{eqnarray}
よって、\((アx+イ)(x-ウ)\) : \((2x+5)(x-2)\) となります。
(2)\(c=2\)のとき、①は以下のようになります。
\begin{eqnarray} & & 2x^2+(4\cdot2-3)x+2\cdot2^2-2-11 \\ &=& 2x^2+(8-3)x+8-13 \\ &=& 2x^2+5x-5 = 0 \end{eqnarray}
この左辺は因数分解できませんし、問題の答えの形を見てもこれは二次方程式の解の公式を使えということでしょう。
はい、呪文です。にーえーぶんの まいなすびー ぷらすまいなす るーと びーじじょう まいなす よんえーしー
$$ x=\displaystyle\frac{-b\pm\sqrt{b^2-4ac}}{2a} $$
絶対覚えましょう。白くま父さん未だに覚えていて唱えられますよ。で、適用しますと①の解は以下のようになります。
\begin{eqnarray} x &=& \displaystyle\frac{-5\pm\sqrt{5^2-4\cdot2\cdot(-5)}}{2\cdot2} \\ &=& \displaystyle\frac{-5\pm\sqrt{25+40}}{4} \\ &=& \displaystyle\frac{-5\pm\sqrt{65}}{4} \end{eqnarray}
よって、\(\displaystyle\frac{-エ\pm\sqrt{オカ}}{キ}\) : \(\displaystyle\frac{-5\pm\sqrt{65}}{4}\) となります。
つぎに、大きい方の解を\(a\)にするということですので、
$$ a=\displaystyle\frac{-5+\sqrt{65}}{4} $$
となります。よって、\(\displaystyle\frac{5}{a}\)は以下のようになります。
\begin{eqnarray} \displaystyle\frac{5}{a} &=& \displaystyle\frac{5\cdot4}{-5+\sqrt{65}} \\ &=& \displaystyle\frac{20(5+\sqrt{65})}{(-5+\sqrt{65})(5+\sqrt{65})} 有理化 \\ &=& \displaystyle\frac{20(5+\sqrt{65})}{-25+65} \\ &=& \displaystyle\frac{20(5+\sqrt{65})}{40} \\ &=& \displaystyle\frac{5+\sqrt{65}}{2} \end{eqnarray}
したがって、\(\displaystyle\frac{ク+\sqrt{ケコ}}{サ}\) : \(\displaystyle\frac{5+\sqrt{65}}{2}\) となります。
さて、それでは \(m<\displaystyle\frac{5}{a}<m+1\) をみたす整数\(m\)を求めます。
\(\displaystyle\frac{5}{a}=\frac{5+\sqrt{65}}{2}\)の中で\(\sqrt{65}\)が整数でなく邪魔くさいのですが、\(\sqrt{64}=\sqrt{8^2}=8\)なので、\(\sqrt{65}\simeq8\)と考えてよいです。
よって、\(\displaystyle\frac{5}{a}=\frac{5+\sqrt{65}}{2}\simeq\frac{5+8}{2}=6.5\)となります。
したがって、\(m<6.5<m+1\)ということですから、\(m<6.5\)と\(6.5<m+1\)と分けて考えると、\(m<6.5\)と\(5.5<m\)となりますので、\(5.5<m<6.5\)となり、コレを満たす整数は\(m=6\)ですね。
よって、シ : 6 となります。
ーーー

答えは、ス : 3 となります。
ーーー
①の解が異なる2つの実数解を持つようなcの値の範囲は、2次方程式の解の判別式でわかりますので、それを求めてから、有理数つまり解の根号が外れるようなcの値を求めていけばいいでしょう。
まずは、解の判別式適用です。
また呪文です。びーじじょう まいなすよんえーしー
\begin{eqnarray} (4c-3)^2-4\cdot2\cdot(2c^2-c-11) \\ = 16c^2-24c+9-16c^28c+88 \\ = -16c+97 &>& 0 \\ 97 &>& 16c \\ 6.0625 &>& c \end{eqnarray}
ということで、cは1〜6の値を取るということですね。さて、あとは根号の中が整数の自乗の形になっていれば、有理数になりますね。
根号の中つまり、\(-16c+97\)の\(c\)に1〜6を代入して調べていきましょうか。
| \(c=\) | 1 | 2 | 3 | 4 | 5 | 6 |
| 根号の中 | 81 | 65 | 49 | 33 | 17 | 1 |
| 2整数の自乗か? | \(9^2\) | x | \(7^2\) | x | x | \(1^2\) |
ということで、①の解が異なる二つの有理数であるような正の整数\(c\)の個数は ス : 3 個である。となります。
他にも大学共通テストの解答の記事がありますので、よかったら見てくださいね。

初稿:2021-3-8




コメント