

答えは④です。
この問題と解くには放物運動について理解しておく必要があると思います。
放物運動に関しての知識は、下記の動画がよく説明されていますので、よかったらご覧ください。20分くらいですよ。
NHK高校講座 基礎物理
第7回 第1編 物体の運動とエネルギー 投げられた物の運動 ~放物運動~
ーーー
それでは解答です。
この問題は、速度のベクトル図を書いて考えたほうが、わかりやすいですね。
AさんとBさんが同じ高さの時の速度のベクトル図が図の上図になります。
\(x\)方向の速度は等速直線運動ですから、変わりません。
\(y\)方向の速度は等加速度直線運動ですが同じ高さですから、\(v_{Ay}=-v_{By}\)です。
だから、\(v_A=v_B\)、\(θ_A=θ_B\)なんですね。
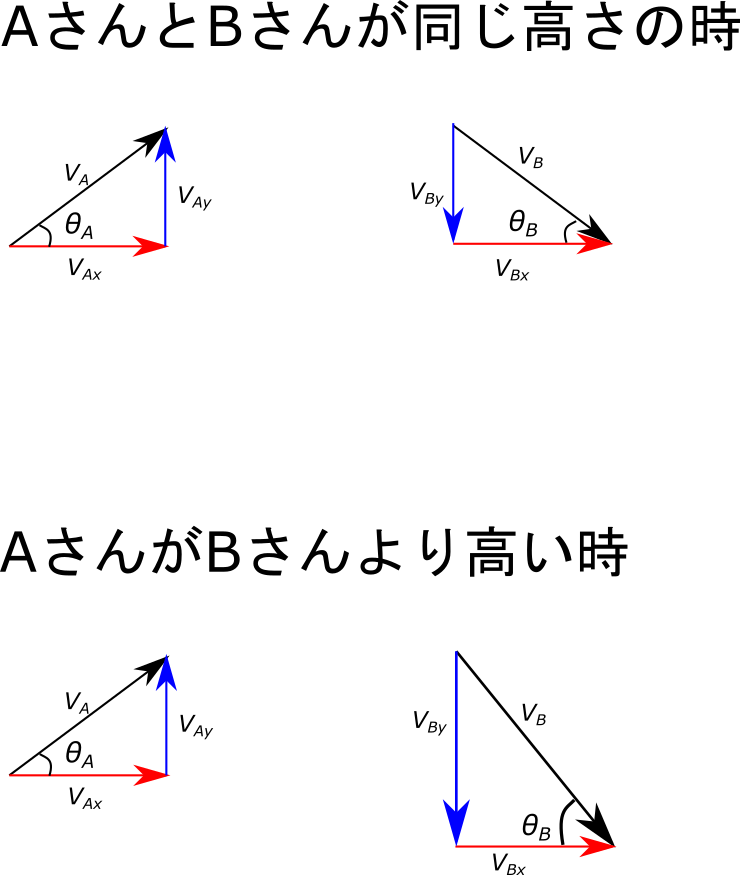
AさんがBさんより高い時の速度のベクトル図が図の下図になります。
\(x\)方向の速度は等速直線運動ですから、変わりません。
\(y\)方向の速度は等加速度直線運動ですから、低い位置にあるBさんに向かって落ちてきた速度のほうが、Aさんの投げた時の速度より大きくなっていますので、\(v_{Ay}<-v_{By}\)です。
なので、\(v_A<v_B\)、\(θ_A<θ_B\)となり、答えは④となります。
ーーー

答えは、問2:③、 問3:① です。
これらの問題は、運動量保存の法則、力学的エネルギー保存の法則、あとは三角関数やベクトルの知識が有れば解けます。
力学的エネルギーに関しての知識は、下記の動画がよく説明されていますので、よかったらご覧ください。20分くらいですよ。
NHK高校講座 基礎物理
第19回 第1編 物体の運動とエネルギー なくならないエネルギー ~力学的エネルギーの保存~
ーーー
それでは解答です。
まずは、問2です。
そりとBさんとボールが一体になってすべる運動は、水平方向の運動を考えることになります。
Bさんが届いたボールを捕球した際、ボールの速度\(v_B\)のうち、問1の解説の図の\(v_{Bx}\)成分が水平方向です。
\(v_{Bx}\)は、\(v_B\)と三角関数を用いて、\(v_{Bx}=v_B\cosθ_B\)と表せます。
こういう物体の衝突の問題は、運動量保存の法則をつかうと簡単に速度を求めることが出来ます。
Bさんが補給する前のボールの水平方向の運動量:\(mv_{Bx}=mv_B\cosθ_B\)
そりとBさんとボールが一体になってすべっている時の運動量:\((m+M)V\)
捕球する前と後で運動量が保存されますので、\((m+M)V=mv_B\cosθ_B\)となり、\(V=\displaystyle\frac{mv_B\cosθ_B}{m+M}\)と捕球した後のBさんの速度がもとめられます。
よって、問2の答えは③となりますね。
三角関数を用いたベクトルの成分表示は慣れておいたほうが良いですよ。
次に、問3です。
水平方向の運動を問2で考えましたね。
Bさんがボールを捕球して、ボールとそりとBさんが一体になって滑っていきました。
これは典型的な完全非弾性衝突の状態ですから、運動エネルギーが失われています。
さらに、ボールの垂直方向の運動は、捕球後のBさんの運動に寄与してませんので、ここでも運動エネルギーが失われています。
ということで、\(ΔE\)は負の値となります。
もちろん、失われたエネルギーは熱などになっています。
よって、問3の答えは①となります。
これはサービス問題ですかね。
ーーー
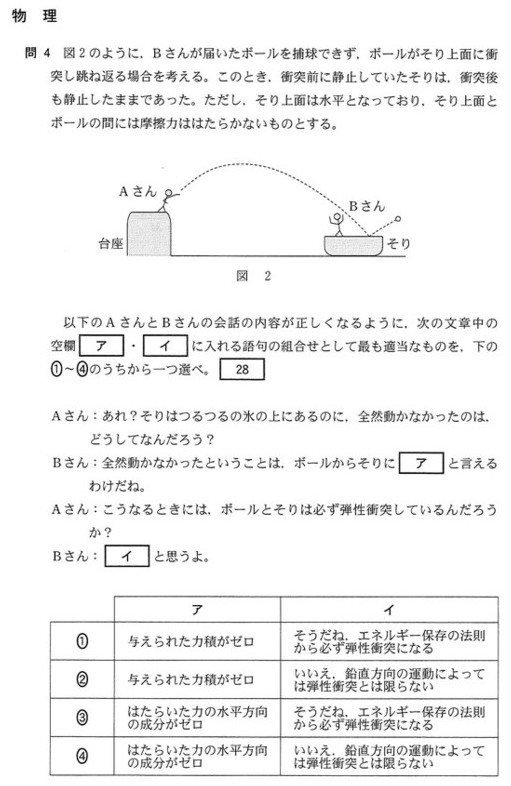
答えは④になります。
この問題は、力積、弾性衝突、非弾性衝突、力学的エネルギー保存の法則について理解している必要があります。
ーーー
それでは解答です。
ボールがそりに当たって跳ね返っていますので、ボールはそりから力積を受けていますし、作用反作用の法則でそりもボールから力積を受けています。
よって、選択肢①②は消えます。
アは、はたらいた力の水平方向の成分がゼロということになり、この解答も矛盾はありませんので、選択肢は③④にしぼられます。
衝突の際、完全弾性衝突になることよりも、非弾性衝突になることのほうが多く、自然界はほとんど非弾性衝突となります。
完全弾性衝突であれば、問題文に衝突の前後で速度が変わらないとか、同じ高さまで跳ね返った等々、力学的エネルギーが保存されている条件があるはずですが、とくにありませんので、弾性衝突になるとは限らないととらえるのが妥当だということになります。
よって、答えは④となります。
他にも大学共通テストの解答の記事がありますので、よかったら見てくださいね。

初稿:2021-2-27




コメント