
答えは、7:③、8:⑤ です。
波の周期と振動数(周波数)の関係の知識を問う問題です。
また、各音階には、基本となる振動数の他に2の整数倍以上の振動数の倍音が含まれることも知っておくとよいかもしれません。
ーーー
それでは解答です。
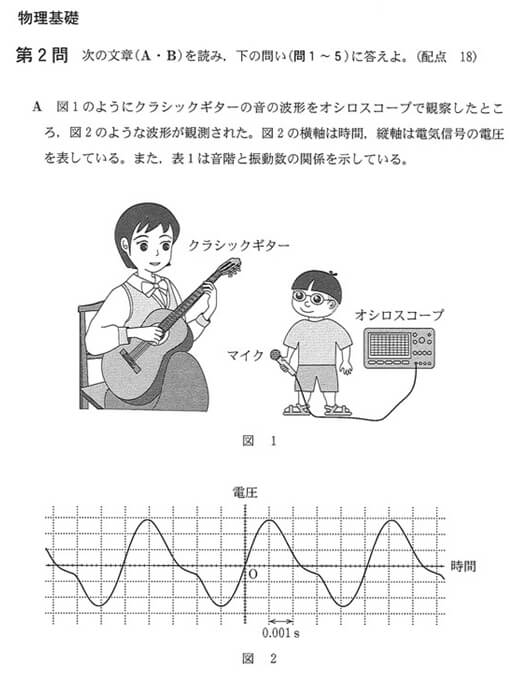
図2から、波形の周期を読み取り、周波数を求めます。
より正確にもとめるには1周期分の波形を読むよりも、なるべく多くの周期を読み取り、平均を取るのが一般的に良いです。
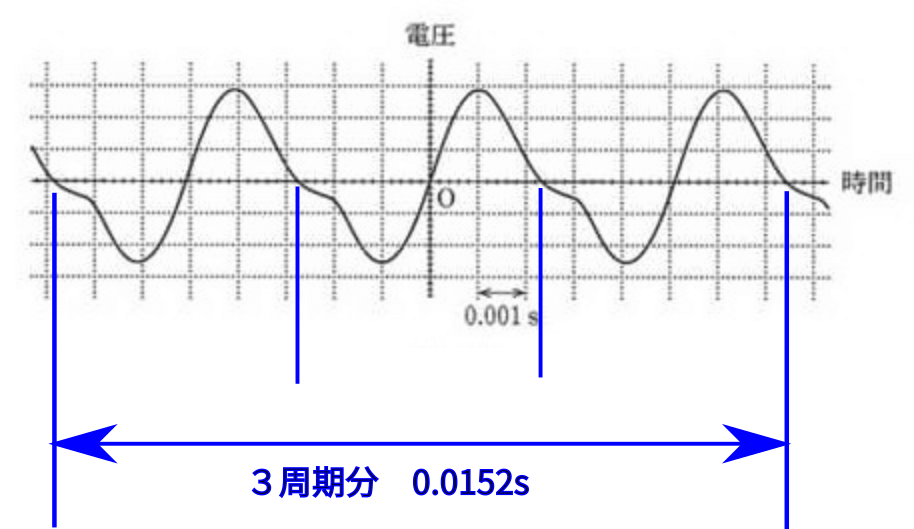
$$ 0.0152s \div 3 \simeq 0.00507s $$
よって、7の選択肢の中で最も近いのは③0.0051となります。
この波形の周期が0.0051sと求められましたので、この波形の振動数(周波数)は\(振動数 =\displaystyle\frac{ 1}{ 周期}\)で求められます(一秒間に何周期分の波形があるかを計算する=振動数(周波数)を求めることになるわけですね)。
$$ 振動数 =\frac{ 1}{ 周期} =\frac{ 1}{ 0.0051s} \simeq 196Hz $$
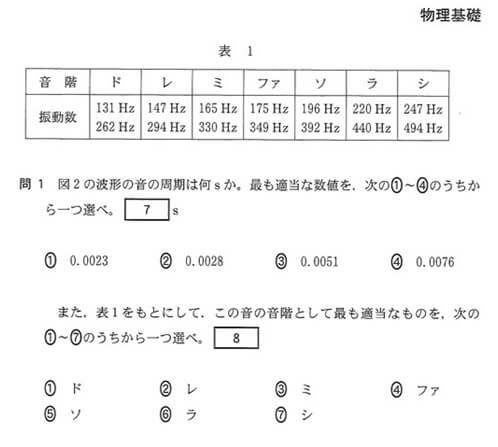
表1をみると、196Hzが含まれる音階は「ソ」ですから、8:⑤が正解となります。
ーーー
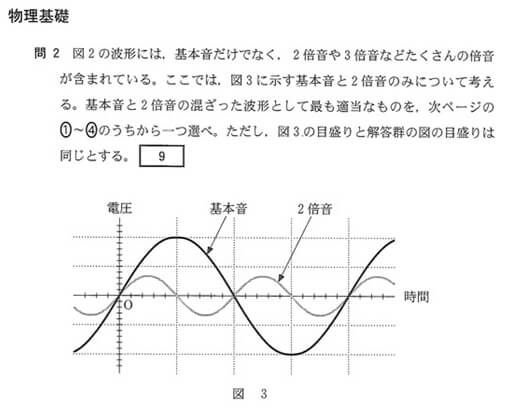
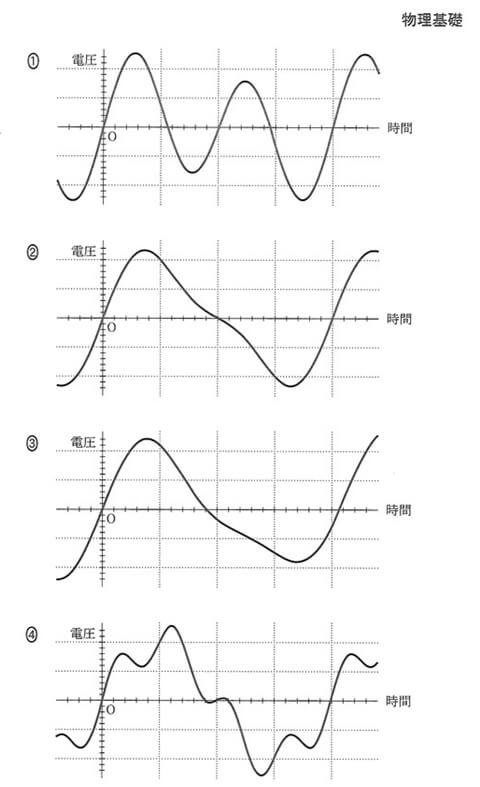
正解は②です。
基本音と2倍音を単純に値を足した時の波形を選択することになりますよ。
ーーー
それでは解答です
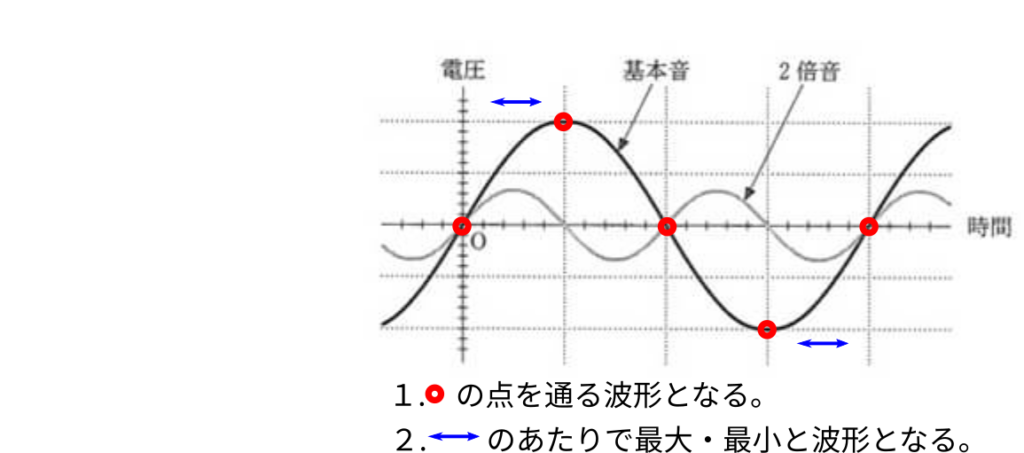
2倍音が0になる時間に、基本音の振幅と同じになる1.の条件を満たす波形になるはずですから、①と③は消えて、②か④にしぼられます。
基本音と2倍音の波形を足すと、2.の条件の期間で最大・最小となる波形が正解ですから、④は消えて、②が正解となります。
他にも大学共通テストの解答の記事がありますので、よかったら見てくださいね。

初稿:2021-1-27
数式修正:2021-2-22




コメント